web课第二个项目，这个比较水，代码目测就100行多点，不过我自己分析的部分比较多。。继续丢实验报告上来。。。

实验内容

实现 spectral clustering等几个社区发现算法,并比较实验结果;

实验环境

• 编程语言为Matlab
• 运行环境OS X El Captain
• 使用工具：Matlab 2015b，matlab_BGL 4.0

实验步骤及方法

以下列出各个算法的大致实现方法

1. GN算法

GN算法是一种分裂型的社区发现算法，我在本实验中的实现大概如下：

1. 计算各边的betweenness

2. 去除betweenness值最高的边

3. 计算该图的连通片

4. 判断连通片的数目compsize，若小于k，转1

2. alink-jaccard算法

alink－jaccard是一种层次聚类方法，它使用jaccard相似度作为节点间的"距离"，再使用聚类算法，初始时每个节点为一个cluster，每次迭代将cluster间节点距离平均值最小的两个cluster合并，直到剩下k个cluster为止。

3. rcut算法

rcut是基于谱聚类的一种方法，可以把社区发现的问题转换成求矩阵特征向量，再在特征向量上使用kmeans算法。 定义矩阵\(D\)为图的度矩阵，\(W\)为图的邻接矩阵，则拉普拉斯矩阵\(L = D - W\) 求这个矩阵的特征向量，把它按从小到大的顺序排列，取前k个特征向量，在上面使用kmeans算法得到聚类结果。

4. ncut算法

实现方法基本同rcut，只是这里定义的拉普拉斯矩阵为 \(D^{- \frac 12} (D-W) D^{- \frac 12}\)

5. modularity算法

modularity算法在这里的实现方法类似谱聚类的方法，这里定义\(B=A-dd^T/2m\),\(A\)为图的邻接矩阵，\(d\)为顶点度数向量，即\(d_i = degreeof(node_i)\)，\(m\)为图的边数，这里可以用A矩阵的非零元素数目/2来获得。 该算法求B矩阵的特征向量，选择其中最大的k个向量来做kmeans算法。

实验结果说明及演示

1. polbooks数据集

以下是实验过程中得到的nmi及acc值：

nmi值是一种聚类间的准确度测量，取值范围为[0, 1]，1表示两聚类之间完全匹配。

这里nmi和acc最高的都是rcut，最低的都是modularity。

结果和我预想的不太一样，我是觉得modularity、rcut、ncut都是基于谱分析的聚类算法，nmi、acc应该比较接近，而且modularity是直接对Q值进行迭代优化，nmi应该不会低，然而实验结果与我想的不太一样，可能的原因是kmeans算法初始取的点位置不太好，结果收敛到了局部最优值，导致聚类效果的下降。

这里的算法中，modularity、rcut、ncut都使用了kmeans算法，所以得到的结果都不太稳定。

GN算法每次选取betweenness 最大的边删除，也是分裂式的聚类方法，每次删除一条最不重要的边，和两个cut的算法差不多，但cut的算法每次找的是图的一个割，按边删除可能在最终得到聚类上和标准答案有些差距，但总体表现得不错。

alink层级聚类方法是不断合并相似节点，最终得到聚类。聚类内部应该是比较相似的，但是聚类之间的距离可能不如其他算法那么明显。

2. football数据集

从得到的结果看来，这个数据集上进行聚类的效果远差于上一个数据集，可能是因为这个数据集有12个社区，距离较近的节点可能属于不同的社区，这个数据集上还是rcut表现得最好，可以看出，三个使用了kmeans的算法的acc要略高一些，可能是因为社区的区域出现重叠的缘故。而nmi值，除了modularity略低一些之外，其他四个算法都差不多，可能是modularity在寻找比较小的社区时的效果不是太好。

3. egonet集k值的确定

egonet数据集中未给出k值，我这里对于k值的确定是基于这样的考虑：当k值小于正确的社区数时，每个聚类的半径，即聚类中的点离该类中心最远的距离，它随k值的增大而减少，减少幅度应该是很大的；而当k值大于实际社区数时，聚类半径随k值增加的下降会变得很慢，甚至上升。

所以我这里确定k值的方法是对每个k值，使用rcut的L矩阵得到对应的特征向量，选取第2～4个特征向量，相当于将数据集映射到三维空间。再在这上面运行kmeans算法，这里的k值设为1～10，之后记录每个k值对应的k个聚类半径的加权平均值sumdist(k)（按聚类大小加权）。最后将sumdist中的k个值绘制成图，图中斜率变化最大的那个点就是理想的k值

先在给定了k值的polbooks数据集上做测试，得到图：

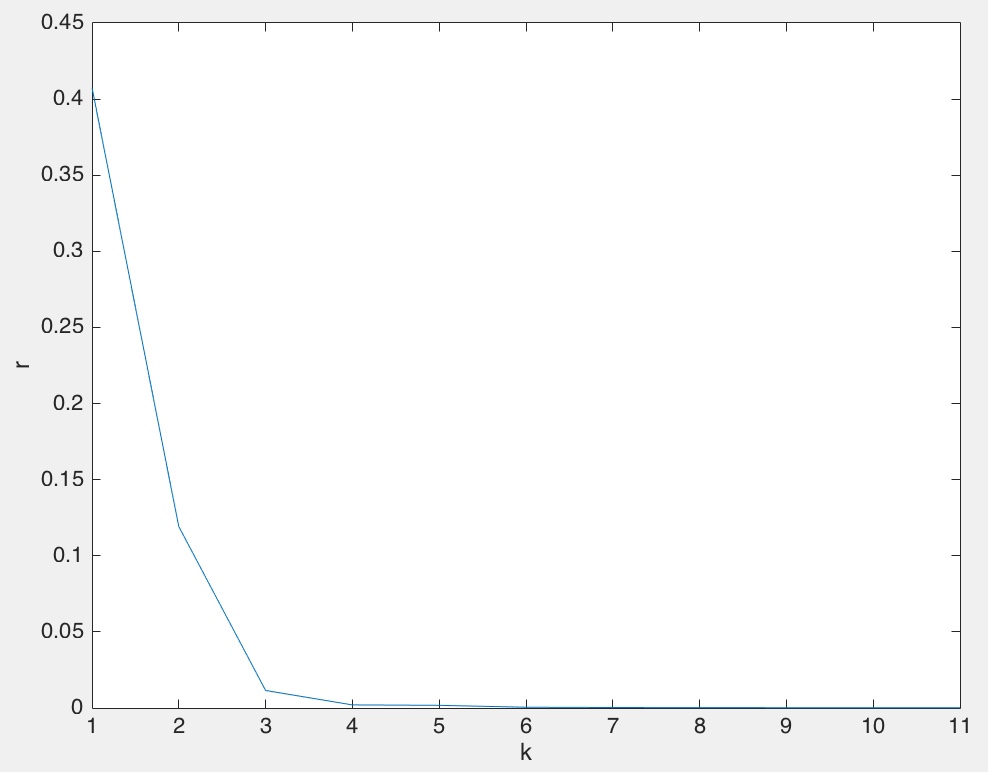
可以看到，当k ＝ 3时斜率变化最大，在这个数据集上的k值确实为3

再在DBLP数据集上测试：

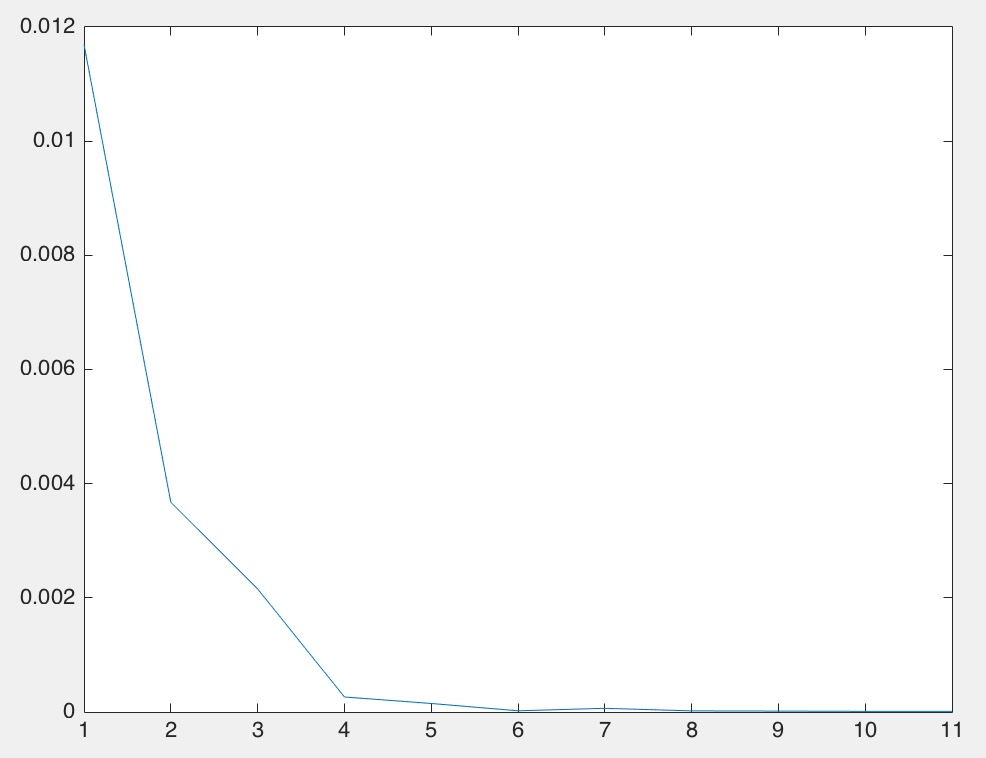
可以发现，图中结果表示k值应取4.

最后，在egonet数据集上运行：

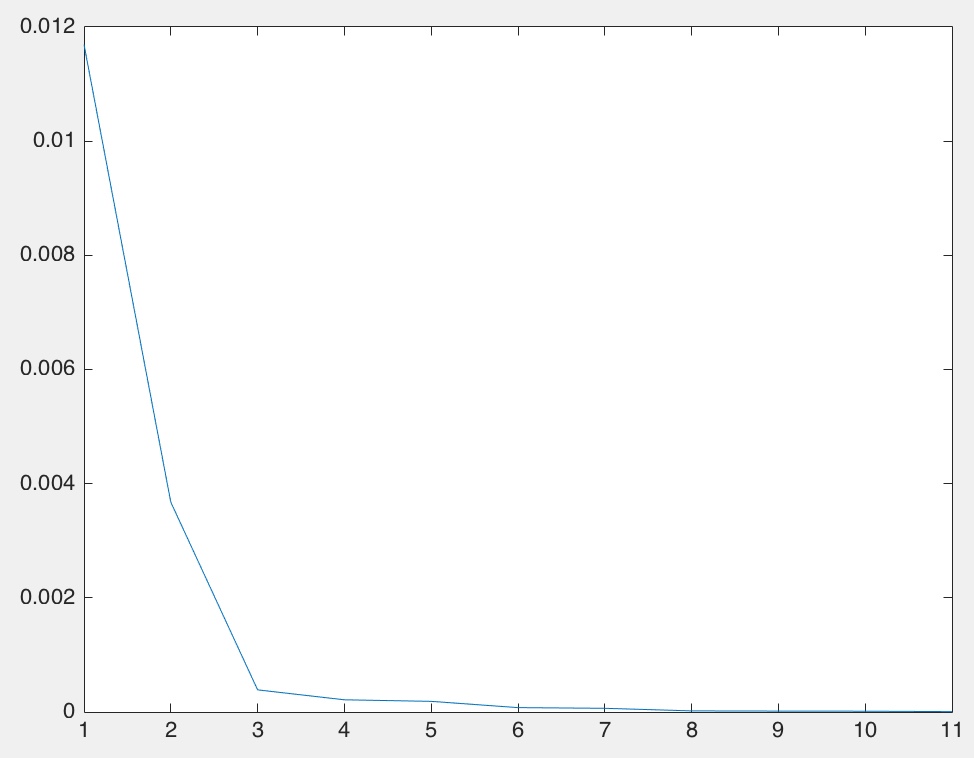
从图中看出，k应该取3.

下面附上选定k值的脚本源码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

function testrcut(A)
W = A;
wsize = size(W);
D = zeros(wsize);
for i = 1:wsize(1)
    D(i,i) = sum(W(i,:));
end

L = D - W;
[x, ~] = eig(L);

ksize = 10;
kstart = 1;
sumdist = zeros(1,kstart+ksize);
for k=kstart:kstart+ksize
    r = zeros(1,k);
    clusize = zeros(1,k);
    V = x(:, 1:3);
    [clustering,~,~,sumd] = kmeans(V, k);
    for i = 1:wsize(1)
        r(clustering(i)) = max(r(clustering(i)),sumd(i,clustering(i)));
    end
    for j = 1:k
        clusize(j) = length(find(clustering == j));
    end
    sumdist(k) = sum(r.*clusize)/sum(clusize)/k;
end
plot(sumdist);
end

这个实验在几个数据集上运行了5个比较经典的聚类算法，让我熟悉了进行社区发现的基础知识。实验所用的Matlab语言比较适合矩阵的运算，也有很多高效的工具包来完成距离计算等功能。在此次实验中，可以发现这些聚类算法对于距离近的节点属于不同社区的这种情况的效果不是很好，对于小社区的发现的效果也不是很好，这些地方应该存在更为有效的解决方案。