立方数码问题

又一个学期过去了，我已经成为一只大四狗。。没有课的生活真是爽，想了想我还有这么一个blog，打算把上学期学到的东西、做的实验整理一下，造福后人～

先写写上学期做的AI实验吧，上过AI课的应该都知道一个经典问题－8数码问题，立方数码问题就相当于8数码问题的三维版本，具体的要求如下（嗯我直接截图好了）：

要求输出最短的移动操作序列

代码可见 https://github.com/xymeow/AI-course-lab1/tree/master/27digits

1. 估计值

估计值h1为当前立方体中错位的方格数，h2为曼哈顿距离，即每个数字到其目标状态的三个方向距离之和。

2. A*算法

A*算法即启发式的广度优先搜索，维护OPEN表和 CLOSE表，每次从OPEN表中访问耗散值f最小的节点，先查找是否已经出现在CLOSE表中，若已在CLOSE表中则不访问。若不在，访问过后将此节点插入到CLOSE表中。

数据结构：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


direction：方向枚举
enum direction {
    LEFT,
    RIGHT,
    UP,
    DOWN,
    FORWARD,
    BACK,
    NONE
};

Point：点坐标
typedef struct Point {
    int x;
    int y;
    int z;
}Point;

Node：状态节点
typedef struct Node {
    char status[28]; //当前立方体状态，前27个分别对应27个方格中内容
    Node *parent; //当前状态的父节点
    Node *next; //同一耗散值的下一个状态
    int f; //耗散值f
    int g; //深度g
    int h; //估计值h
    Point blank; //空格位置
    direction movement; //得到当前状态所做的操作
    friend bool operator < (const Node a, const Node b) {
        return a.f >= b.f;
    } //比较函数
}

Node OPEN[MAXLEN+1]; //OPEN表，使用一个桶

map<Node, int> CLOSE;  //CLOSE表，用stl中的map实现

下面是我做的一些优化：

OPEN表的实现: 用结构数组＋链表实现了一个桶状数据结构，数组中的每个下标为当前的f值，插入时将节点放入对应的桶中，若当前节点f值比全局变量currentf值更小时，修改currentf = Node.f。弹出时从currentf所指的那个桶中取出一个节点，并修改OPEN表。使用这样的数据结构比优先队列要快一些。具体实现可见insert/top/pop函数
防止重复移动: 记录每个节点的移动操作，若操作与父节点的相反（DOWN和UP相反，BACK和FOWARD，LEFT和RIGHT），则剪枝。
内存分配: 用VISIT数组记录所有的状态，每当状态超过VISIT数组的长度时，将VISIT长度增长为2倍，避免每访问一个节点就要进行一次内存分配，提高速度。

其他的实现可见代码文件

3. IDA*算法

算法伪代码如下：

具体的实现可见代码文件，嗯我比较懒，而且算法我也没做啥优化，和上面的伪代码差不多。。。

下面是A*和IDA*的时间－规模图（选取了Ah1能跑出结果的移动步数）：

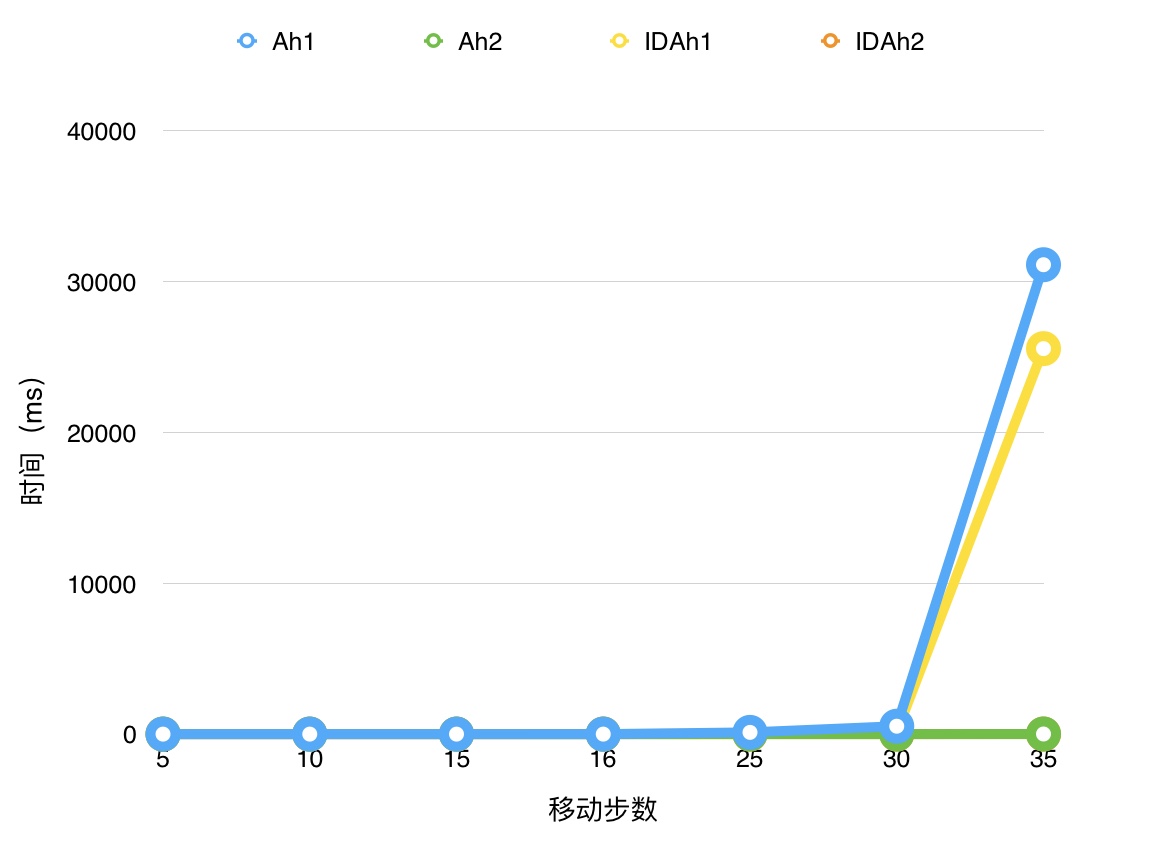
可见，在所用时间上，IDAh2<Ah2<IDAh1<Ah1，选对估计函数很重要哇复杂度不好估计。在空间上，由于IDA算法只用记录深度优先遍历中将要访问的节点，可以近似认为是\(O(step)\)的而A算法需要记录所有访问过的节点，故空间复杂度是\(O(2^{step})\)的，所以跑步数比较多的测试用例时内存基本都会炸。。。

然后还有一个改进的IDA算法，当每次搜索达到阈值时，不是退回到根节点重新搜索，而是记住边缘的节点，从边缘处再开始，我记得好像是叫边缘IDA

Contents

1. 估计值

2. A*算法

3. IDA*算法